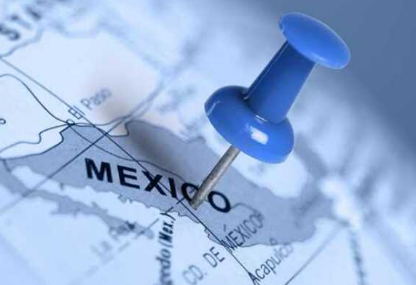
如图$∠A=∠B=90^{\circ}$$E$是$AB$上的一点且$AE=BC$$∠1=∠2$．(1)$Rt\triangle（ADE$与$Rt\triangle BEC$全等吗 并说明理由； (2)$\triangle CDE$是不是直角三角形 并说明理由．","title_text":"如图$∠A=∠B=90^{\circ}$$E$是$AB$上的一点且$AE=BC$$∠1=∠2$．(1)$Rt\triangle ADE$与$Rt\triangle BEC$全等吗 并说明理由； (2)$\triangle CDE$是不是直角三角形 并说明理由．）

想必现在有很多小伙伴对于如图，$∠A=∠B=90^{\circ}$，$E$是$AB$上的一点，且$AE=BC$，$∠1=∠2$．(1)$Rt\triangle ADE$与$Rt\triangle BEC$全等吗 并说明理由； (2)$\triangle CDE$是不是直角三角形 并说明理由．","title_text":"如图，$∠A=∠B=90^{\circ}$，$E$是$AB$上的一点，且$AE=BC$，$∠1=∠2$．(1)$Rt\triangle ADE$与$Rt\triangle BEC$全等吗 并说明理由； (2)$\triangle CDE$是不是直角三角形 并说明理由．方面的知识都比较想要了解，那么今天小好小编就为大家收集了一些关于如图，$∠A=∠B=90^{\circ}$，$E$是$AB$上的一点，且$AE=BC$，$∠1=∠2$．(1)$Rt\triangle ADE$与$Rt\triangle BEC$全等吗 并说明理由； (2)$\triangle CDE$是不是直角三角形 并说明理由．","title_text":"如图，$∠A=∠B=90^{\circ}$，$E$是$AB$上的一点，且$AE=BC$，$∠1=∠2$．(1)$Rt\triangle ADE$与$Rt\triangle BEC$全等吗 并说明理由； (2)$\triangle CDE$是不是直角三角形 并说明理由．方面的知识分享给大家，希望大家会喜欢哦。

(1)全等，理由是： $∵∠1=∠2$， $∴DE=CE$。

$∵∠A=∠B=90^{circ}$，$AE=BC$， $∴Rttriangle ADE$≌$Rttriangle BEC$；